Hydrogenic model of an impurity in a semiconductor

The simple model for a hydrogen atom can be used to describe the behaviour of an impurity in a semiconductor. Thus the formula for the ionisation energy of a hydrogen atom,

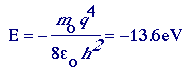
and the radius of the lowest orbit of the electron around the hydrogen nucleus

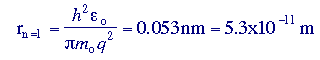
can be applied in modified form to calculate how an electron or hole will interact with its parent impurity atom. mo and eo are replaced by m^* (effective mass) and respectively since we are now concern with charge embedded in a semiconductor and not in vacuum (or free space).

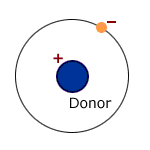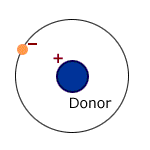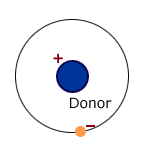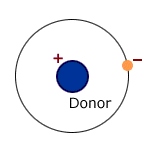
Figure 1: Spare electron orbiting the donor impurity at T = 0K.

In the case of a donor impurity, the single electron which is not required for covalent bonding is assumed to orbit the impurity at low temperatures , remaining close to the donor through coulombic attraction between its own negative charge and the positive charge of the corresponding proton in the nucleus of the impurity. Its orbit radius is

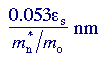
and its ionization energy becomes

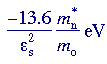
Thus the orbit radius is much larger than that of the hydrogen atom, and the ionisation energy energy significantly smaller. For example , r_n=1 = 1.25nm and |E| = E_D = 50meV for an electron-donor system in silicon. This small ionisation energy means that the electron escapes from the influence of the impurity at fairly low temperatures to become a free , conduction band electron. We are therefore justified in assuming that all donor impurities in silicon are ionised at room temperature, 300 K , and n_o = N⁺_D = N_D.